※この記事は自分の学習と効率化のために、ChatGPTに書いてもらったものをベースとしています。
画像と赤文字で記載されている箇所などは私のコメントや感想部分です。
7.実験計画法と特殊なグラフタイプ
ANOVA (分散分析) の基本
ANOVAは、3つ以上の群間での平均の違いを検定するための統計的手法です。特に、実験計画法の中で、異なる条件下での結果が統計的に有意に異なるかどうかを評価するためによく用いられます。
一元配置ANOVAは、1つの因子のみが影響を及ぼす場合に使用されます。一方、二元配置ANOVAは、2つの因子が影響を及ぼす場合に用いられます。
ANOVAの前提として、各群のデータが正規分布に従う、各群のデータの分散が等しい、といった条件が必要です。
前のトピックくらいから怪しくなってきましたが、この説明はマジで一切わからん。。
ということで、再度GPT先生に一元配置ANOVAの具体例を聞きました。以下回答
一元配置ANOVA(One-way ANOVA)の具体例として、「肥料の種類が植物の成長に与える影響」を検討する場合を考えます。
背景
農学の研究者が3種類の異なる肥料(A、B、C)がトマトの植物の成長に与える影響を調べたいとします。肥料はそれぞれが異なる栄養成分を含んでおり、研究者はどの肥料がトマトの成長(例えば、植物の高さ)を最も促進するかを知りたいと考えています。
実験デザイン
トマトの苗をランダムに3つのグループに分けます。
各グループにはそれぞれ肥料A、B、Cを使用します。
実験は同じ条件下で行われ、すべての苗は同量の水と日光を受け取ります。
8週間後に、各植物の高さを測定します。
データ収集
各肥料グループから複数の植物の高さを測定し、以下のようなデータが得られたとします。
肥料Aを使用した植物の高さ:[40, 42, 43, 41, 39 cm]
肥料Bを使用した植物の高さ:[38, 37, 35, 36, 36 cm]
肥料Cを使用した植物の高さ:[45, 43, 44, 46, 47 cm]
ANOVAの実行
一元配置ANOVAを使用して、3つの肥料グループ間の平均高さに統計的に有意な違いがあるかどうかを検定します。
群間変動:各グループの平均高さの違いに基づく変動。
群内変動:各グループ内の植物の高さのばらつきに基づく変動。
結果の解釈
ANOVAの結果、得られたF値が批判値よりも大きい場合、またはp値が0.05以下である場合、3つの肥料グループ間に統計的に有意な差があると結論づけます。
これは、少なくとも一つの肥料が他の肥料と比べてトマトの成長に異なる影響を与えていることを意味します。
追加の多重比較
ANOVAで有意差が見つかった場合、TukeyのHSDテストやBonferroni補正などの多重比較手法を使用して、具体的にどの肥料グループ間に違いがあるのかを調べます。
このように一元配置ANOVAは、一つの因子について複数のレベル(条件)が従属変数(この場合は植物の高さ)に与える影響を統計的に評価するのに有効な手法です。
GPT先生
なんとなく、さっきより理解は出来ましたが。追加の多重比較のところは「ちょっと何言ってるのかわからない」
極座標プロットや3Dプロットを使用してデータを可視化
極座標プロット:
極座標プロットは、2次元平面上で放射状にデータを表示するためのグラフです。例えば、風の方向や強さを表示する際などに用いられます。
import numpy as np
import matplotlib.pyplot as plt
# サンプルデータ
theta = np.linspace(0, 2*np.pi, 100)
r = 2 + np.sin(5*theta) # データを生成
fig, ax = plt.subplots(subplot_kw={'projection': 'polar'})
ax.plot(theta, r)
ax.set_title("Polar Coordinate Plot")
plt.show()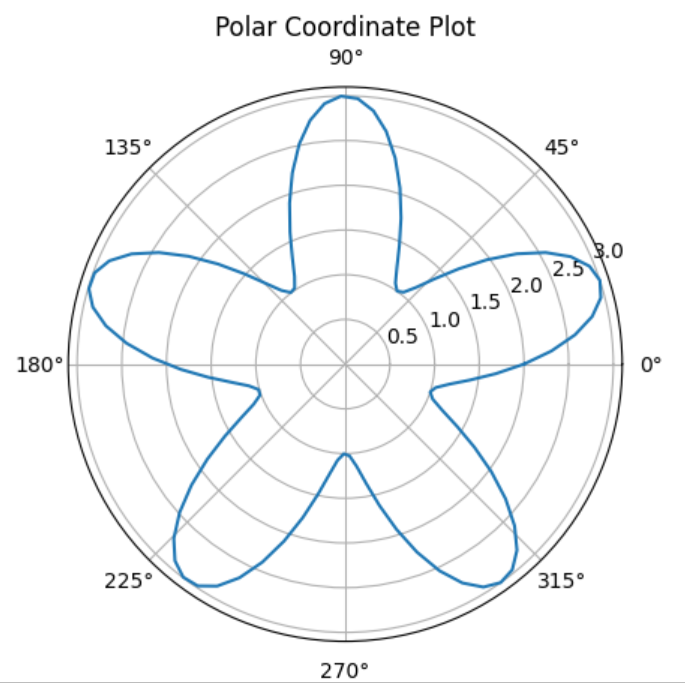
3Dプロット:
3Dプロットは、3つの変数の関係を可視化するためのグラフです。
from mpl_toolkits.mplot3d import Axes3D
# サンプルデータ
X = np.linspace(-5, 5, 50)
Y = np.linspace(-5, 5, 50)
X, Y = np.meshgrid(X, Y)
Z = np.sin(np.sqrt(X**2 + Y**2))
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_title("3D Surface Plot")
plt.show()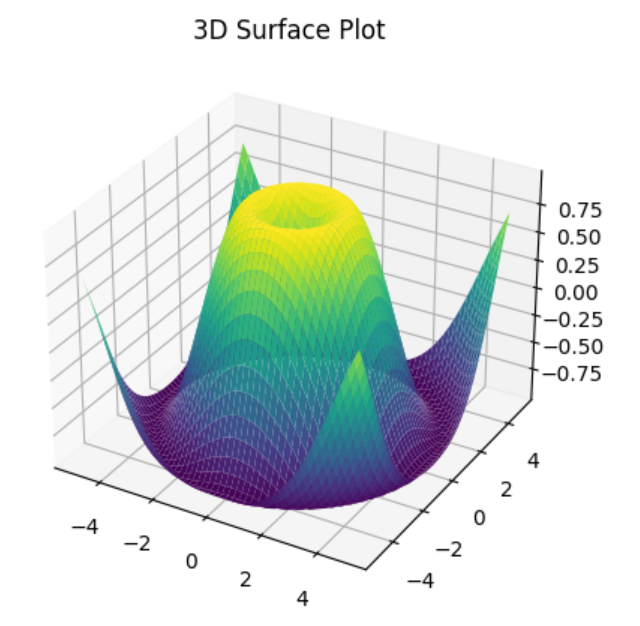
このコードでは、3Dの曲面プロットを表示しています。plot_surface: メソッドを使用して、3つの変数X, Y, Zの関係を3D空間上にプロットしています。
この記事では、実験計画法の一つであるANOVAの基本と、matplotlibを使用した特殊なグラフタイプのプロット方法について学びました。




